Nano is small. Yet we find that a few nanoparticles can have very large scale effects. How do we make sense of these disparate scales? Several previous blog posts — such as this, this, and this — have provided great insight to this question. But as a chemistry professor I know that you can never have too many ways of trying to understand the nanoscale, so here is yet another back-of-the-envelope calculation to reveal just how small nano is.
Let’s start with the definition of nano. It’s the inverse (opposite) of a billion. An American billion is 10 to the power of 9. That’s a 1 with NINE zeros after it: 1,000,000,000. Nano is 1 part of that billion. That’s .000000001 which has a lot of zeros, too.
What does that tiny number mean? Let’s start by imagining a cube with 100 beads on each edge:
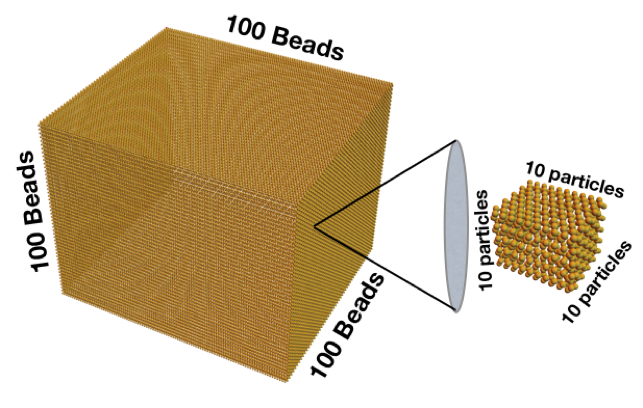
That cube is made of 1 million beads. If every one of those beads represents a cube with 10 particles along each edge, then you would have a billion particles. The catch to understanding how small a nanometer is is that, instead of putting all of those particles in a cube, we need to put them all in a line like ants walking in single file. The billion particles all lined up would be a meter stick, and one tiny individual particle is the nanometer. A nanoparticle in three dimensions has that width of 1 in a billion in each direction. That makes its volume 1 in 10 to the power of 27. That’s a lot more zeros, and why a nano volume is so small.
How small a space does that nanoparticle occupy? If we assume a simple nanometer cubed, how much space is that and how many atoms fit inside of it? For the answer, let’s have a little coffee. Or rather, let’s look at 3/5 of a shot of espresso:

If we remove the caffeine and all the other stuff that makes it coffee, we are left with 3/5 (or 0.6) of an ounce of water. After factoring the density of water (1g per cm cubed) and taking care of units, you’ll find that that the volume of our water shot is about 18 x 1021nm3. The one thing that I didn’t tell you is that I chose that volume because it just so happens that it is precisely the volume of a mole of water molecules. The mole is a very large number — about 6 x 1023. Also called Avogadro’s number, it is so important to chemists that we like to hang out with the mole at our national chemistry meetings:

We also celebrate today, October 23 (1023) as Mole Day!
So if we divide 18 x 1021nm3by 6 x 1023, we find that one water molecule occupies .030 nm3 in volume. Since every molecule of water (known chemically as H2O) has three atoms (two hydrogen atoms and one oxygen atom), that means one atom has a volume of .010 nm3 . One nanometer cubed is 100 times that volume, and hence would accommodate roughly 100 atoms.
Actually, 1 nanometer cubed of any substance would contain around 100 atoms. If it’s a nanoparticle, unlike a molecule, they are stuck together not by chemical bonds but by mutual attraction. They can, of course, be a little bigger or a little smaller than 100 atoms. But they can’t be too much bigger as we need to keep the lengths on the order of nanometers. If it were to be too big, you would lose the nanoscale and then it wouldn’t be a nanoparticle any longer. Hopefully you will never have to find a single nanoparticle in 3/5 oz of espresso, though. That would be a one in 600,000,000,000,000,000,000,000 shot!
