Two years ago, I wrote a blog post called Two Ways to Make Nanoparticles, describing the difference between top-down and bottom-up methods for making nanoparticles. In the post I commented, “we can estimate, knowing how gold atoms pack into crystals, that there are about 2000 gold atoms in one 4 nm diameter gold nanoparticle.” Recently, a Sustainable Nano reader wrote in to ask about how this calculation is done. It’s a great question!
In order to estimate how many atoms are in a gold nanoparticle, we have to talk a little about crystal structure. Crystals form when atoms (or molecules) arrange themselves in an ordered way in three dimensions. The smallest unit of that structure is called a unit cell. The example below shows a simple cubic structure where there is one atom at each corner of a cube, and the cubes stack together to make the crystal structure.

Gold crystallizes in what is called a face-centered cubic structure. This means that in addition to the corner atoms on each unit cell like the example above, gold also has an atom on the faces of each unit cell, one for each of the six sides of the cube. These are shown in green on this drawing:

It might be confusing to count how many atoms there are in a gold unit cell. There are 8 atoms sitting on the corners of the unit cell, and 6 atoms that sit on each face of the unit cell. But you have to imagine that this unit cell is stacked on top of other unit cells, is under other ones, is next to other ones, on and on in all directions.
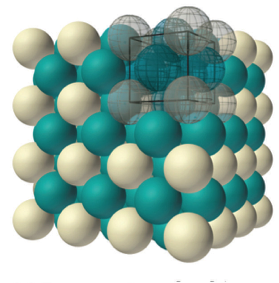
So that means that the 8 atoms on the corners of each unit are shared by the units above, below, and next to it! It turns out that each unit shares its corner atoms among a total of 8 unit cells, and those green face atoms are also each shared between two adjacent unit cells.
Therefore, if we want to count how many atoms are in ONE gold unit cell, we have to only count the pieces of the atoms that are in that one unit cell.
- Since each corner atom is only 1/8 inside our unit cell, but there are 8 corners, 8 x (1/8) = 1.
- Since each face atom is only half inside our unit cell, but there are 6 of them, 6 x (1/2) = 3.
- 1+3 = 4, so there are 4 total atoms per unit cell.
Now we are ready to think about nanoparticles!
Let’s dust off some geometry skills. X-ray crystallography experiments tell us that the unit cell edge length for gold is 0.408 nanometers. The unit cell is a perfect cube, so its volume (length x width x height) is 0.4083= 0.0679 cubic nm.

Even though the unit cells of gold nanocrystals are cubic, gold nanoparticles themselves are pretty much spherical in shape. If we consider a 4 nm diameter gold nanoparticle to be a sphere with a radius of 2nm (remember radius = half of diameter), then its volume is 4/3 πr3= 33.5 nm3.

Now that we know the nanoparticle’s volume, we have to figure out how many unit cells of gold will occupy that amount of space. This calculation is easy: we divide the volume of the sphere by the volume of the gold unit cell: 33.5/0.0679 = 493 (approximately).
If we want to make our lives easier, we can just round this up to 500 unit cells per nanoparticle.
We already know from the crystal structure of gold that there are 4 atoms per unit cell. Since there are about 500 unit cells per nanoparticle, this means we have about 4 atoms x 500 unit cells = 2000 gold atoms per nanoparticle!

Please keep sending in those reader questions! Just click the “Ask the Scientists” button on the left.
EDUCATIONAL RESOURCES
- SERC at Carleton College: Directed Discovery of Crystal Structures by David Mogk and Kent Ratajeski
- National Council of Teachers of Mathematics activity on dimensions & volume: Popcorn Anyone?

[…] our 10 nanometer diameter gold nanoparticle contains about a quarter million gold atoms (see how to calculate that number in a recent Sustainable Nano blog post), and hundreds of those nanoparticles would barely cover the […]