gchong3

Happy Mole Day 2016!

Happy Mole Day from the CSN! This is our third annual post for Mole Day (check out the posts for 2014 and 2015), so it is starting to become a tradition now. In this post, I will show you an example of a real pen-and-paper calculation involving moles that I do sometimes in my work as a theoretical and computational chemist. This calculation will help us answer a question: How many water molecules do I put in a 70 Å x 70 Å x 70 Å box containing a 4 nm gold nanoparticle?

Molecules
Cathy Murphy calculated in a previous post that there are ~2,000 gold atoms in a 4-nm-diameter gold nanoparticle. The 4 nm particle on the left has 2,123 atoms to be exact. Keep reading to find out how many water molecules are in the images in the center and the right!   (image by Gene Chong)

As a quick reminder, the mole is an SI unit used to count the number of atoms or molecules in a substance (similar to how a minute is a unit used to measure how many seconds of time have occurred). A mole of any element on the periodic table contains 6.022 x 1023 (also known as Avogadro’s number) atoms. This unit is used so often in chemistry that chemists celebrate it on October 23rd from 6:02 AM to 6:02 PM.

Why isn’t Mole Day on June 2 from 10:23 AM to 10:23 PM? I’m guessing it’s because school would be out. I remember my high school chemistry teacher celebrated Mole Day every year and held contests, such as best drawing of a mole (the animal) doing chemistry, to get us excited about chemistry. On a grander scale, the American Chemical Society deems the week of Mole Day as National Chemistry Week (this year it was last week, since Mole Day was on Sunday). They designate a different theme each year and provide educational resources and activities for students to get more engaged in the subject. Recent themes have included “Nanotechnology: The Smallest BIG Idea in Science!,” “The Sweet Side of Chemistry: Candy,” and this year’s “Solving Mysteries Through Chemistry.” Click on the links for suggested classroom activities, such as creating a secret message using disappearing and appearing ink and determining which fruit juice products contain artificial food dye.

mole
A mole! (Not the chemistry kind.)  (image by Kenneth Catania)

Getting back to the subject of Moles: classroom experiments are usually done in beakers, i.e. in large volumes. It would be silly to talk about how many thousands of trillions of molecules of whatever are in those beakers. Instead, typical units for concentration used in such experiments would be moles per liter. For computational chemists trying to understand how atoms and molecules behave, current technology allows us to access up to a few thousand computer processors that can collectively work to model a few million atoms at most. But remember, a mole of atoms means 6.022 x 1023 atoms! That means I am unable to model either moles of material or liters (or even milliliters) of water, and so obviously I can’t model both combined! In a simulation, every atom needs to be labeled and tracked, so a common unit of concentration for us to model is the number of atoms or molecules per cubic angstrom, or Å3. (Note, 1 m = 1010 Å and 1 cm3 = 1 mL). However, even though our volume is very tiny, we still need to make sure that it matches the density of water (1000 kg/m3 or 1 g/cm3). We want to simulate reality, after all.

So the volume of my simulation box is 343,000 Å3. That’s 3.43 x 10-22 liters! Could you imagine dividing a 2-liter bottle of soda among 68,600,000,000,000,000,000,000 people? Using the formula for the volume of a sphere, we know the volume of the 4-nm spherical nanoparticle is 4/3 x π x (20 Å)3. Therefore, the volume available for water is the volume of the simulation box minus the volume of the nanoparticle.

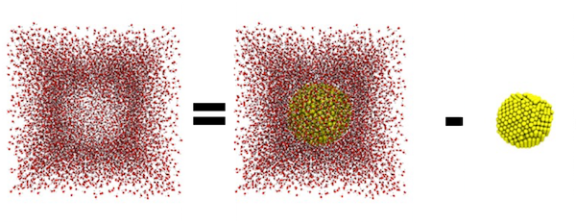
Volume of water
To figure out the volume of water in the simulation box, we take the overall volume of the box minus the volume of the spherical nanoparticle.   (image by Gene Chong)

Now for those who just want to know the answer to the main question, multiply the density of water by the water volume we just determined to find the mass of the water. Then, to convert mass of water to moles of water, divide by the molar mass of water (the mass that we know contains a mole of water molecules). Finally, multiply by Avogadro’s number to get the number of water molecules to place in the simulation box! Here’s what all of that looks like:

equationSo the answer is that if I want to simulate a 4-nm gold nanoparticle in water inside a 70 Å x 70 Å x 70 Å box at the right density, I will have to add 10,354 water molecules to my computer model.

This is a simplified version of what I do. Now, suppose I coat the surface of the nanoparticles with some crazy molecules that act like patches of Velcro, and I want to know how these new “decorated” nanoparticles stick together in solution. Then, I would choose a box size big enough to fit these particles and follow the same calculation to figure out how many water molecules to add. And lastly, I run the simulation to predict what might happen when people actually make them!

EDUCATIONAL RESOURCES