Seeing small objects is no simple task, but it is an essential one for scientists from fields as diverse as astronomy and nanotechnology. In order to see tiny things, we need to both magnify them and keep their fine details apparent. Which is more important, raw enlarging power or precise detail?
To help me explain, I will use a high resolution and low resolution version of the same image of HONORARY DOG OF SCIENCE Jackson to demonstrate this concept!

As you will instantly notice, that is a gorgeous mutt. Next, the pictures on the left show magnification and high resolution, while the photos on the right show magnification without increased resolution. At low magnification (that entire lovable face, top images), there is little difference between the two pictures. This is because we are looking from far enough away that we can’t even see the resolution limit (the point at which we lose the fine details). In the bottom two pictures however, the picture on the left maintains the fine detail, while the one on the right does not. This means we have reached the resolution limit in the image on the right.
Putting Some Numbers to It
If I look closely at my dog’s nose, I can see slightly more detail than in the images in the left column. By measuring the spaces between details on my dog’s nose, I can determine roughly the resolution limit of the images above. This takes a bit of work and patience, although Jackson is a trooper.

The little ridges on his nose lie less than 1 mm apart. Since these ridges are apparent in the images in the left column and not apparent in those on the right, this means that the images in the left column have a resolution limit smaller than 0.1 mm, while those on the right have a resolution limit larger than 0.1 mm. You may recall that in the most zoomed-out picture (again that handsome face!), the resolution limit did not matter. In this specific case, resolution is not that important as we are not looking closely enough to see the details.
While bigger is often better, magnification can be meaningless if the necessary resolution is lacking as Jackson once again demonstrates.

So, resolution is the ability of a system to define detail, and this becomes increasingly important the more you magnify something. What if you magnify something A LOT? What are the limits to resolution?
How to Push the Limits?
There is a fundamental maximum resolution for a system that is determined by a process known as diffraction. When light enters a lens, it diffracts, spreading out and making a spot in an object into a slightly larger disk in the image. If two spots in an object are too close, their image disks overlap, and we cannot see the two unique features (see Ian’s post for more). When the resolution is only limited by diffraction, the distance needed between objects in order for them to be seen as separate (ΔL) is given by the equation
where D is the aperture size (typically the size of the largest lens) and λ is the wavelength of electromagnetic radiation used (in this case visible light). From this mathematical relationship, we can see the best resolution or smallest distance between distinguishable objects (small ΔL) occurs by using a really large lens (big D) or very small wavelengths of electromagnetic radiation (small λ).
Often the choice depends on the application, although with nanomaterials, visible light wavelengths (λ ranges from 400 for blue to 700 nanometers for red) are too big to resolve details smaller than their own wavelength. Therefore, nanoscientists turn to electrons. These subatomic particles have wave-like properties, and in electron microscopes their wavelengths can be as low as 2.5 picometers (over 100,000 times smaller than visible light)! This is the core principle of how electron microscopes produce images like those below (look for a more in depth discussion in an upcoming blog post on how electron microscopes work!). A byproduct of using electrons instead of visible light to image something is that the resulting images have no color. Below are two images I took using our scanning electron microscope.

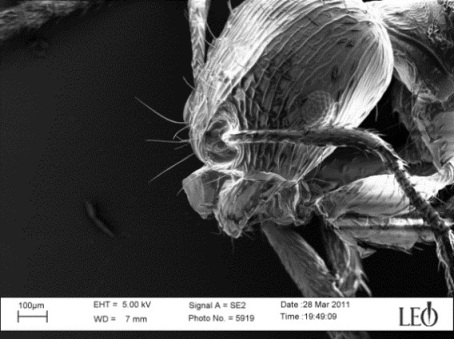
Astronomers pursue a different route to beautiful images. Since astronomers take images of gigantic heavenly bodies that span far more than trillions of miles, they do not need to see nanometer-level detail and probably would prefer images in color. This means they use visible light and other forms of electromagnetic radiation in the imaging process. Since they are stuck with certain wavelengths of light, astronomers increase their image resolution by crafting really huge lenses or mirrors to put into telescopes (increasing “D” in the equation above). A very famous example is the Hubble telescope, which has a mirror that is nearly 8 feet in diameter!


With such a large lens, the amazing becomes possible. The images below are some of the fantastic photos that the Hubble has been beaming back for its last 23 years of operation. The image on the right is one of the most famous images taken by the Hubble of the Horsehead Nebula in the constellation Orion, which is located a mere 1500 light years away (or approximately 14,000,000,000,000,000 kilometers)! The resolution of this image is roughly 34.2 billion km1 (a byproduct of how extremely far away the nebula is).


So, is magnification or resolution more important?
In Conclusion…
Well, while magnification and resolution are completely different things, they have a dependent, intertwined relationship. Magnification is often critical in scientific research, but only if you can achieve a resolution sufficient to see all the fine detail in which you are interested. For this reason, scientists require both magnification and resolution, although different scientists go about achieving resolution in different ways. In the end, like most situations in life, it is good to have a little bit of everything, the right resolution for the right magnification. With the right combination of the two, some pretty amazing pictures are possible. Hopefully I have cleared things up a bit because Jackson and I are spent. Happy Science-ing!
Super-Technical Footnote of Science:
I calculated the resolution of the horsehead nebula image using the theoretical best angular resolution for the Hubble telescope, which is 0.5 arcsec or 0.00014 degrees. I then used the geometry of a right triangle to determine the lateral resolution of the image, meaning tan(0.00014)=x/(distance to nebula) and solved for x.
![CropperCapture[26]](https://sustainablenano.files.wordpress.com/2013/12/croppercapture26.jpg?w=723)


[…] Para leer el blog original en ingles, presione aquí. […]
[…] 5 – Acquire a series of images and spend a few hours at home with your dog of science, painstakingly stitching the images together into the big composite image you see at the top of […]
Reblogged this on Spock's Sister Sees and commented:
I had to reblog this. It has a dog-of-science 😀
Thanks for sharing! Hopefully your readers love Jackson!