Happy Nano Day, Everyone! Though you might be looking at me weird if you use the dd/mm dating system, tomorrow (10/9 in the U.S.) is the day to celebrate the scale that’s minuter than micro and more prodigious than pico.
So what is Nano Day? Nano Day, or National Nanotechnology Day, is a celebration started by the National Nanotechnology Initiative (NNI) to celebrate all the advancements that nanomaterials have brought us. But why did they settle on October 9th? The answer comes from the use of scientific notation and how it relates to metric prefixes.

What is Scientific Notation?
Scientific notation is a way of writing extremely large OR extremely small numbers more clearly and concisely. For example, which is easier to read at a glance: 5,320,000,000,000 or 5.3 trillion? Scientific notation is a sort of mathematical shorthand, in which our example would be written as 5.3 x 1012.
For this to make sense, it helps to remember that those little superscript numbers (like the 12 in 1012) are exponents. That means you’re multiplying the number by itself that many times: for example 24 = 2x2x2x2 = 16. So in the previous example, 10x10x10x10x10x10x10x10x10x10x10x10 = 1012.

One special thing about exponents of 10 is that you can write them out as just a 1 followed by the exponent number of zeros! So 1012 = 1,000,000,000,000, which is a trillion! There is one special rule when working with exponents, and that is when the exponent is zero. According to the rules we just made, you’d think 100 should equal 0 (10 zero times is 0). However, when you work with exponents, anything raised to the power of 0 is 1. (Here’s a deeper explanation if you’re interested.) This applies to all numbers, not just 10. So 20, 50, and 100 all equal 1, and so on.
So scientific notation uses these handy features of exponents of 10 (sometimes called powers of 10). How it works is that you start with a very large or very small number, and move the decimal point either to the left or right so there’s only one digit remaining ahead of it. Then count the places you moved the decimal point, to find out how many “times 10s” you need to take into account.
For example, the decimal point is implied but invisible at the end of our 5.3 trillion example, so we’d move it like this, 12 places to the left:
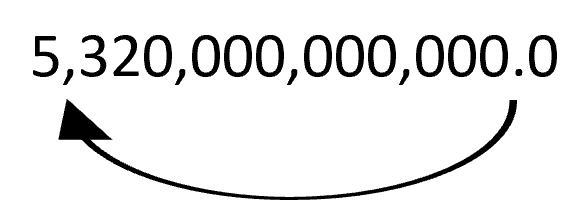
If we had a really small number like 0.000002513 (about two hundred millionths), we’d move the decimal point like this, 6 places to the right:

When you move the decimal place to the left, the exponent is positive and that means it’s a big number. So our first example in scientific notation would be 5.32 x 1012. When you move the decimal point to the right, the exponent is negative, meaning it’s a tiny number – our second example in scientific notation would be 2.513 x 10-2.
Why is Nano Day 10/9?
So, coming back to Nano Day: what makes October 9th symbolize nano? This is where metric prefixes come in. These are a series of prefixes we use to help quickly describe the scale of a unit of measurement. You may be familiar with some like milli (think millimeter or millisecond) or kilo (like kilometer or kilogram).
The most common prefixes range from the billions to the billionths, each representing a specific exponent or power of ten:
| Prefix | Power |
| Giga- | 109 |
| Mega- | 106 |
| Kilo | 103 |
| Hecto- | 102 |
| Deka- | 101 |
| Base | 100 |
| Deci- | 10-1 |
| Centi- | 10-2 |
| Milli- | 10-3 |
| Micro- | 10-6 |
| Nano- | 10-9 |
| Pico- | 10-12 |
There’s nano way down at the bottom! 10-9 gives us 10/9 or October 9 for Nano Day!
Fun with exponents
To give some scale to these prefixes, let’s put them in terms of lengths. The base for length in the metric system is the meter (m) which is a little longer than a yard, so about the height of many doorknobs. You could write 1 meter as 1 x 100 in scientific notation, but you probably wouldn’t bother because that’s the same as writing 1 x 1.

Going larger you have the kilometer (km, 103) which is equivalent to a little over half a mile. Many humans can run multiple kilometers at a time, like 5k or 10k races you might have watched in the Olympics this past summer. Larger than that are megameters (Mm, 106) which could be used to describe the size of medium to large countries, and gigameters (Gm, 109), which start to describe the size of planetary bodies. Our sun makes a good example, with a diameter of 1.3 Gm; the distance between the earth and the sun is 150 Gm!

On the other end of the spectrum, going through the prefixes for tiny numbers we start getting closer to nano. Centimeters (cm, 10-2) are finger size and useful for everyday measurements, and your hair is roughly the size of a millimeter (mm, 10-3). Next are micrometers (μm, 10-6. There are just too many m-abbreviations so we use the greek letter mu here.) Micrometers are on the scale of bacteria and cells, so small we need a microscope to see them. Finally, we hit nanometers (nm, 10-9), the size of the particles we work with in the CSN. They’re around the size of a virus or your DNA. Stuff so small you can’t even see it with a regular microscope because it’s smaller than wavelengths of visible light!
So, we can see that Nano Day was placed on the ninth of October because nano represents the billionth scale or 10-9. It seems fair to also say that today is Giga Day, but it might be better to hit up NASA about that one. If you want to find out different ways that you can celebrate, you can find some great ideas on the NNI website, like running a 100 Billion Nanometer Dash. You can also find some more suggestions on our blog, such as making nano s’mores or contemplating how nanoscience relates to a pint of beer or even chocolate. Whatever you do, I hope this post gives you a new appreciation for the uses of scientific notation in nanoscience and our everyday life.
