Molecular music: Patterns of vibrations at the quantum level

Hearing of the fire at Notre Dame de Paris a year ago broke my heart. I have only been there once in my life, but that visit is one of my most cherished memories. Before studying chemistry and joining the Center for Sustainable Nanotechnology, I earned a music education degree, with a major in voice and a minor in piano. I sang in a choir that toured France my senior year. We visited and sang in some of the most beautiful cathedrals, but the one that impacted me the most was Notre Dame de Paris. Its stained glass is breathtaking, and I could almost feel the centuries of Catholic history those walls have witnessed.

*Notre Dame de Paris, taken in 2011. The vaulted ceilings and reflective stone made for great acoustics. (photo by Laura Kesner)*

Have you ever heard a choir singing in a cathedral? It’s so beautiful. It’s really an unparalleled sound you just have to experience in person at least once in your life if you can. The vaulted Gothic architecture in many European cathedrals is more than just visually beautiful—it carries and beautifies the sound. The massive stone walls and arches reverberate, or reflect sound so that it bounces all around, lasting seconds after the source stops. This reverberation smears the sound together a little, like the blending of paint colors. This actually brings out notes that may otherwise not be noticeable, because they weren’t actually sung or played. They are overtones, which our Center director talked about in this blog post regarding overtones and color. Watch this video and note both the reverberation from the room and the overtones produced from just a few voices.

Overtones are found in a variety of things: sounds, colors, and even quantum mechanics. Quantum mechanics may sound intimidating, but don’t let it scare you. It’s like cat logic: my cats like attacking my shirt even when I’m shaking a much nicer feather toy to distract them. Why they prefer playing with my shirt, even when I’ve picked them up and put them next to their real toys, I’ll never really know. The rules of quantum mechanics themselves don’t make a whole lot of sense to us (even to many of the scientists who study it), but accepting what we observe and using those rules does help explain many scientific phenomena, even better than cat logic explains cats!

Overtones in Music

We’ll get back to quantum a little bit later. But first, let’s talk overtones in music. Music is made when vibration of a string, air column, or other part of an instrument (or person!) causes the air around it to compress at specific intervals. The faster these air molecules compress and decompress, the higher the frequency of the sound wave; the higher the frequency, the higher the pitch.

*Sound waves are intervals of compressed air (image from Popular Science, 1878, US Public Domain)*

To see how this applies to overtones on a musical instrument, let’s look at the A string on a violin (the third string from the left):

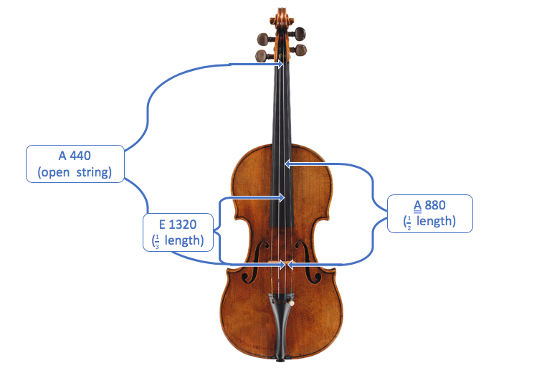
*Lengths that vibrate for A 440, A 880, and E 1320 on the A string on a violin. (image modified from The Henry Ford)*

Shortening the length of the string increases the frequency and raises the pitch: when the length is halved, the frequency is doubled; when the length is divided into three, the frequency is tripled, etc. Making the string longer will likewise decrease the frequency and the pitch. When the A string of a violin vibrates, it produces a note called A 440. (The 440 indicates how fast the string is vibrating: 440 kilohertz or 440,000 cycles per second!) Pressing the string against the fingerboard halfway down the string essentially cuts the string in half, so playing the string doubles the vibration frequency: A 880 (2 x 440). Cutting the string to a third of its original length produces E 1320 (3 x 440).

The note that is played – along with the frequencies we’ve been describing so far – is called the fundamental. But the violin actually produces more notes than just the fundamental, which is why it sounds more interesting than a computer-generated tone: it also vibrates as if its length were divided into 2, 3, 4, and so on. If A 440 is played on the A string, it also produces hints of A 880 and E 1320, and even higher pitches, but they are much softer than the fundamental.

Here’s an example (which we also used in our glacier post!) of a 440 Hz tone generated by a computer, without overtones:

And here’s an example of a 440 Hz musical note played by a violin, including overtones (from the University of Iowa Electronic Music Studios:

So what do these overtones look like in terms of the sound waves we were talking about?

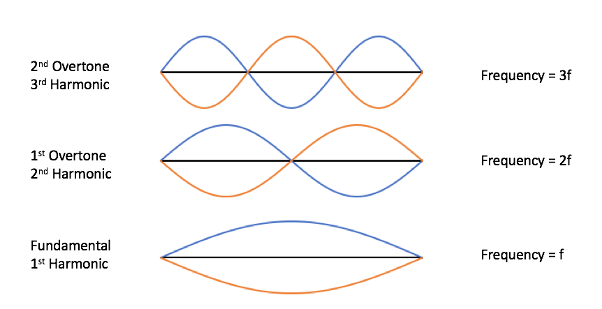
*Vibration patterns and frequencies for the first three harmonics in the harmonic series. (Figure by Laura Kesner)*

These notes are called harmonics: in music, a harmonic is a frequency that is a whole number (1, 2, 3, 4, etc.) multiple of the fundamental pitch, like we saw with the A 440 string example. The sequence of harmonics increasing in frequency and pitch is called the harmonic series. Any higher pitch that is heard in addition to the fundamental is called an overtone. All harmonics except the fundamental are overtones, but some overtones are not harmonics because they aren’t multiples as we’ve been talking about–they have different numerical ratios.

So how does all of this cause that beautiful sound in a stone cathedral? The reverberation makes the overtones more audible, which adds a bell-like ringing quality that is very pleasing to the ear. In a less resonant space, the singers’ voices would still create the same sounds, but the overtones made by those voices will be much quieter.

Overtones also give each type of instrument its unique tone. Different instruments have different overtones that are louder than others, and some even have overtones that aren’t harmonics. It’s based on how the sound is made, the materials, everything about the design of the instrument. While it may be nearly impossible to pick out specific overtones, the result is obvious: when you hear the same note played by a piano, a violin, or any other instrument, you can tell right away which one is which. Try it out! All of the examples below are the same pitch: can you identify the different sources? (answer key below)

example 1

example 2

example 3

example 4

example 5

example 6

example 7

example 8

example 9

example 10

example 11

Quantum Mechanics

This brings us back to quantum mechanics! Quantum mechanics is all about the behavior of electrons within atoms and molecules. Today, we’ll specifically look at the bonds between atoms in a molecule. A molecular bond is like the bond of friendship—it’s a sharing of electrons, rather than a physical attachment. Let’s look at an example molecule of two atoms bonded together:

*An oscillating molecule of two atoms connected by a bond. (Figure by Clyde Daly)*

The bond vibrates like a spring, causing the atoms to oscillate toward and away from each other. The energy of vibration is proportional to the frequency, just like the faster a kitten leaps around, the more energy is involved! Let’s draw a simple graph of the energy states (levels) the electrons of our example can have. We’ll represent each energy state with a horizontal line:

*Vibrational energy levels of an electron. (Figure by Laura Kesner)*

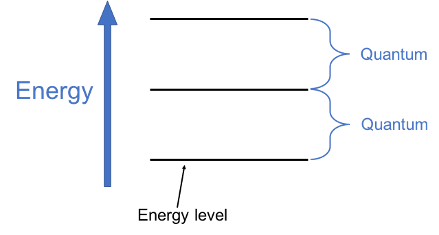
It looks like a ladder, doesn’t it? The amount of energy between each successive energy state is all the same for that bond, like the equal distance between rungs of a ladder. This energy difference is called a quantum, from the same Latin root where we get the word quantity. The size of this vibrational quantum is specific to the combination of atoms, depending on the mass of the atoms and the strength of the sharing of electrons.

When an electron in the bond absorbs vibrational energy in the form of a photon (light particle), it moves to a higher energy state and the frequency increases; when it releases energy, it moves to a lower energy state and the frequency decreases. The energy absorbed or released has to be just the right amount, equal to the difference between the two levels. (Vibrational photons fall within the infrared region of the electromagnetic spectrum.)

This type of vibrational motion is harmonic, meaning that the frequency (the energy level) doesn’t depend on the amplitude (the number of photons). It’s similar to music, where harmonic frequency (pitch) doesn’t depend on how hard the string is played (loudness). (You can play the same note quietly or loudly.) Using “harmonic” for both electron energy levels and music is a loose connection, though; I think the real similarity is much more striking (pun slightly intended). But we’ll get to that: we have a few more things to discuss first!

Quantum Energy Well

Let’s add some more details to our energy level graph. If the molecular bond has more energy, the atoms stretch further apart at their widest point. Let’s change the line width to show this stretching and connect the lines with a smooth curve. Stretching outside this curve would break the bond, but bonds won’t break on their own.

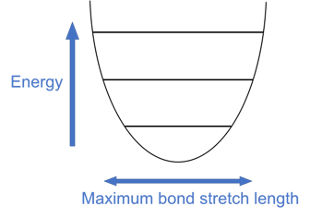
*Energy well showing increasing vibrational energy in the y-axis (vertical) and maximum length that the bond can stretch in the x-axis (horizontal). (Figure by Laura Kesner)*

Here’s where we get to some cat logic: electrons behave like both particles and waves! These electrons are so tiny and are moving so fast that it’s impossible to say for sure where they are (like a blurred image of a car zooming by, only much worse). Instead of pinpointing an electron’s position, scientists use a wavefunction to describe an electron. Wavefunctions are mathematical formulas that describe the energy of electrons and where they might be. Thankfully, for our purposes today we don’t have to know where they came from, or write any equations! Let’s look at the electron wavefunctions mapped onto our energy diagram. Each higher energy level has an additional node (crossing point) compared to the one below it:

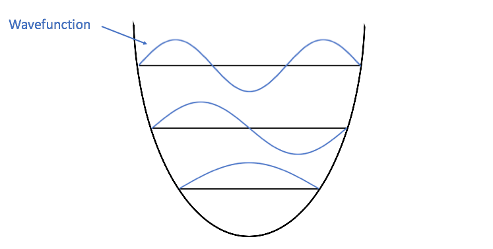
*Energy well with wavefunctions. (Figure by Laura Kesner*)

This pattern looks familiar, doesn’t it? Let’s see the two side-by-side:

*Music harmonic series and quantum harmonic oscillator side-by-side. (Figure by Laura Kesner)*

Perhaps the similarity is only coincidental, but I think the fact that musical harmonics and electron energy levels have same pattern of nodes is really cool. There are some differences, though. Overtones in music are the actual waves made by moving air particles, while the overtones of the quantum harmonic oscillator are formulas that describe the energy of electrons. Also, musical overtones are heard at the same time as the fundamental; in quantum theory, an electron can only have one energy level at any particular time, although the combination of photons from different electrons can produce overtones, like those that produce blue glaciers.

While I find the comparison and overtones in general quite fascinating, I don’t actually think about them when I hear musical overtones: I’m just grateful for the beautiful music they make possible.