The title of this post presents a riddle similar to the one that I solved along with my advisor, Professor Rigoberto Hernandez, in a recent article published in the Journal of Physical Chemistry C.¹ Nanoparticles are often made of a core (for example gold, silver, quantum dots, etc.) coated with molecules called ligands or polymers that protect the core and help the nanoparticles stay suspended well in solution rather than clumping together. You can imagine our polymer molecule as a string of 200 beads. The beads are attracted to the nanoparticle surface, but repulsive to each other. Each bead is sort of attracted to water, but it likes the surface of the nanoparticle more. We know that the polymer molecules stick to nanoparticles, but how?

In order to stick to the nanoparticle surface, our 200 beads have to balance out their attraction to the particle, their relative attraction to water, and their dislike for each other. We can use some holiday imagery to think about the two main options for how they could do this: they could wrap around the nanoparticle like yarn around a ball ornament, or they could loop like a bow on top of  a gift box.

Before I spoil the answer, let’s get some background into how we solved this problem. I’ll share how, as a computational chemist, I use different coordinate systems for describing 3D space to describe the structure of nanoparticles.

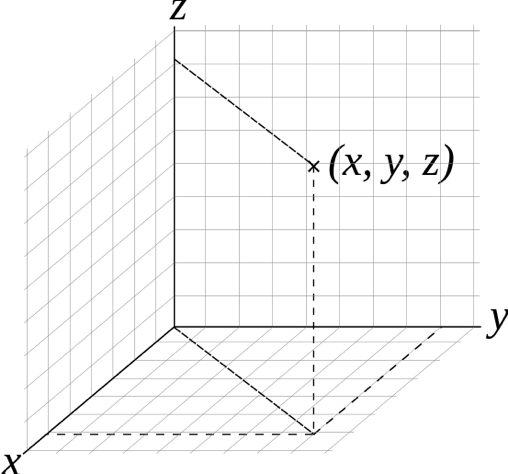
You may be familiar with the Cartesian coordinate system, which describes position in terms of x, y, and z coordinates relative to an origin point (0, 0, 0). So a location that is one unit above, to the right, and in front of that origin point would be labeled (1,1,1).

If you’ve taken a college math course, you may have learned about other coordinate systems; if not, let’s just say that there are other ways to describe position! Spherical and cylindrical coordinate systems are also commonly used to describe the position of an object in three-dimensional space relative to a chosen origin. One main difference between these and Cartesian coordinates is that they use angles as well as distances to describe locations relative to the origin.

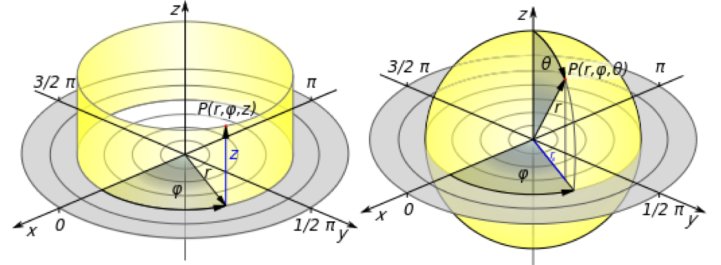
As the name suggests, the spherical coordinate system is useful in describing spherically shaped objects. In this coordinate system, the origin (0, 0, 0) is located at the center of the sphere, and position is described in terms of three new variables (r, φ, θ). The distance from the center of the sphere (in other words, the radius) is r. The φ symbolizes equatorial angle, which goes around the equator from 0° to 360° (also written as 0 to 2π radians) just like the equator on the Earth. The polar angle q is also analogous to a globe, going from 0° at the north pole to 180° at the south pole (or 0 to π radians). (Be careful though; depending on whether you’re talking to a mathematician, physicist, or chemist, the variable for the equatorial angle can be written as θ and the polar angle as φ!)

To help picture spherical coordinates, you can ask yourself: as you go around the equator, where are you between the north and south pole and how far are you from the center? This is really useful when we’re describing where ligand molecules are located on a nanoparticle.

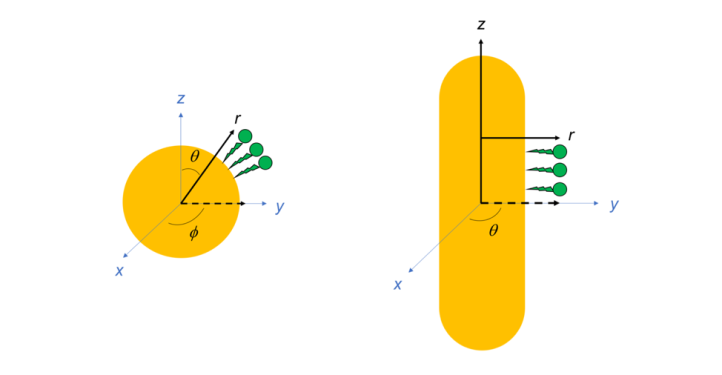
For rod-shaped nanoparticles, a cylindrical coordinate system is useful in describing position along the length of the rod, but we might switch to a spherical coordinate system to describe the hemispherical caps at the ends of the rod. In the cylindrical-coordinate system, position is described in terms of (r, z, θ). Think of this coordinate system as: if the origin (0, 0, 0) is set at the center along both the length and width of the rod and as you go along the length of the rod in the +z or ‑z direction and circle around the z-axis from 0° to 360° (θ), how far is the ligand from the z-axis (r)?

Now with all that explanation out of the way, let’s solve our Holiday Sustainable Nano Riddle.

In our recent article,¹ we used a spherical coordinate system analysis along with some other calculations to show that a 200-monomer polymer attaches to a spherical nanoparticle by looping like a bow on a gift box. We did this by using spherical coordinates to track the positions of nitrogen atoms (colored in blue in the left image below) as they moved in our computer simulation. We found that the polymer does not completely wrap around the particle like in a yarn ball; in that case, the nitrogen atoms would have been positioned across both north and south poles. Instead, we observed that the polymer covers only half the particle, with a high density of nitrogen atoms at the north pole of the nanoparticle.

One way we measure this is by making a “heat map,” shown below on the right. This is like a rectangular map of the world for our polymer, with the colors representing the population density of the monomers or beads in the polymer. The yellows and reds show the densest spots on the heat map, and white indicates a population of zero.And you see that the lower hemisphere is empty!

Although each monomer “bead” is attracted to the nanoparticle surface, it is not likely that they are all crowded on the surface at the north pole of the nanoparticle because all the beads also repel each other. And because the beads are also semi-attracted to water around the particle, as some of them approach and stick to the nanoparticle surface while repelling each other, the whole big polymer buckles, forming loops on the surface.

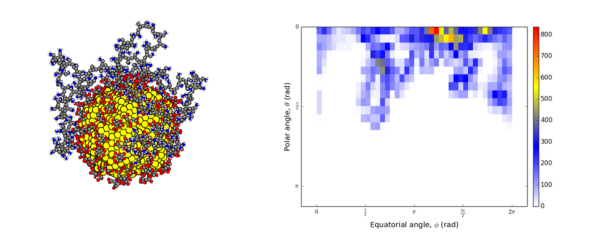
The fact that the polymer didn’t wrap like a ball of yarn was a surprise to us. Why? Because the bow is more structured than the wrapping. More structure means less entropy, and nature usually favors more entropy. In this case, though, the subtle balance between the various interactions between the beads of the polymer and everything else led to the more energy-demanding answer winning. And so, the polymer actually buckles and forms loops like a single bow on gift box.

Happy holidays!

---

REFERENCES

1. Chong, G. & Hernandez, R. Adsorption Dynamics and Structure of Polycations on Citrate-Coated Gold Nanoparticles. Journal of Physical Chemistry C, 2018, 122, 19962-19969. Doi: 10.1021/acs.jpcc.8b05202